Trainable Weight Averaging: Efficient Training by Optimizing Historical Solutions

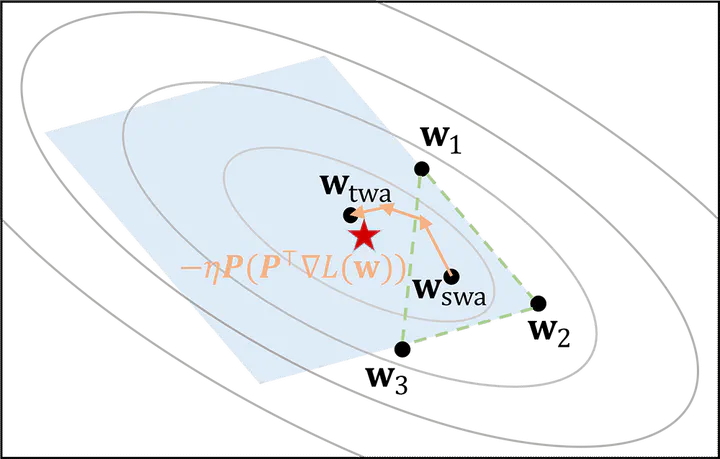
Stochastic gradient descent (SGD) and its variants are considered as the de-facto methods to train deep neural networks (DNNs). While recent improvements to SGD mainly focus on the descent algorithm itself, few works pay attention to utilizing the historical solutions—as an iterative method, SGD has gone through substantial explorations before convergence. Recently, an interesting attempt is stochastic weight averaging (SWA), which significantly improves the generalization by simply averaging the solutions at the tail stage of training. In this paper, we realize that the averaging coefficients could be determined in a trainable manner and propose Trainable Weight Averaging (TWA), a novel optimization method in the reduced subspace spanned by historical solutions. TWA has much greater flexibility and can be applied to the head stage of training to achieve training efficiency while preserving good generalization capability. Further, we propose a distributed training scheme to resolve the memory burden of large-scale training with efficient parallel computation. In the extensive numerical experiments, (i) TWA achieves consistent improvements over SWA with less sensitivity to learning rate; (ii) applying TWA in the head stage of training largely speeds up the convergence, resulting in over 40% time saving on CIFAR and 30% on ImageNet with improved generalization compared with regular training.

In International Conference on Learning Representations 2023