Unified Gradient-Based Machine Unlearning with Remain Geometry Enhancement
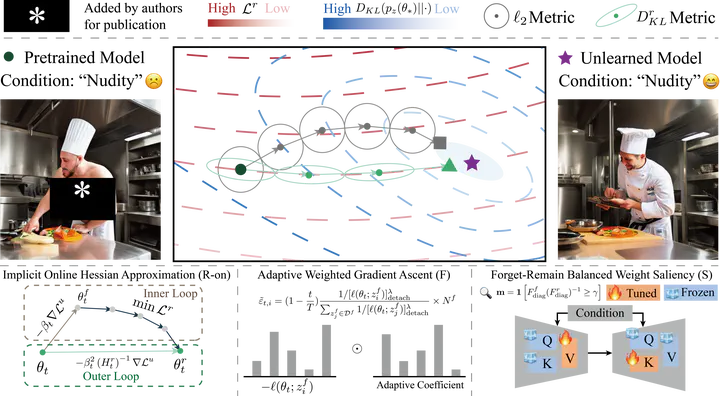Overview of our Saliency Forgetting in the Remain-preserving manifold online (SFR-on).Background
Machine Unlearning (MU) aims to remove the influence of samples from a pre-trained model, ensuring the model behaves as if it has never encountered those samples.
Contributions
- We provide a novel perspective to unify previous approaches by decomposing the vanilla gradient descent direction of approximate MU into three components: weighted forgetting gradient ascent, remaining gradient descent, and a weight saliency matrix.
- We derive the steepest descent direction for approximate MU on the remain-preserved manifold.
- We propose a fast-slow weight method to implicitly approximate online Hessian-modulated salient forgetting updates.
- We conduct experiments on a wide range of CV unlearning tasks across multiple datasets and models of different architectures, verifying the effectiveness and efficiency of our method.
Key Findings
Approximate MU Problem Formulation
The optimization problem of approximate MU at each step can be formulated as:
$$ \begin{align*} &\theta_{t+1} =\mathop{\arg\min}\limits_{\theta_{t+1}} D_{\text{KL}}\left(p_z(\theta_*)||p_z(\theta_{t+1})\right)+\frac{1}{\alpha_t}\rho(\theta_t,\theta_{t+1})\\ &=\mathop{\arg\min}\limits_{\theta_{t+1}} \underbrace{D_{\text{KL}}\left(p_{z^f}(\theta_*)||p_{z^f}(\theta_{t+1})\right)}_{(a)}p^f+ \underbrace{D_{\text{KL}}\left(p_{z^r}(\theta_*)||p_{z^r}(\theta_{t+1})\right)}_{(b)}p^r+ \frac{1}{\alpha_t}\underbrace{\rho(\theta_t,\theta_{t+1})}_{(c)}. \end{align*} $$($a$ ) seeks to eliminate the influence of the target forgetting samples.
($b$ ) aims to maintain the performance on the remaining samples.
($c$ ) employs the metric $\rho$ to constrain the magnitude of each update.
Vanilla Gradient Descent
Under the Euclidean manifold metric, $\rho(\theta_t,\theta_{t+1})=\frac12\lVert \theta_t-\theta_{t+1} \rVert^2$ . The steepest descent direction that minimizes approximate MU is:
$$ \begin{equation*} \theta_{t+1}-\theta_t:\approx-\alpha_t [ \underbrace{H^f_*(H_*^r)^{-1}}_{(S)} \underbrace{[-\nabla \mathcal L^f(\theta_t;\boldsymbol{\varepsilon}_t)]}_{(F)}p^f+ \underbrace{\nabla \mathcal L^r(\theta_t)}_{(R)}p^r ]. \end{equation*} $$Approximate MU in Remain-preserving Manifold
Employing Euclidean distance treats all coordinates as equally important. A practical objective is to constrain parameter updates during unlearning within a manifold that minimally impacts the retained performance.
Using the model output KL divergence on the remaining set as the manifold metric, $\rho(\theta_t,\theta_{t+1})=D_{\text{KL}}\left(p_{z^r}(\theta_t)||p_{z^r}(\theta_{t+1}))\right)$ . The steepest descent direction that minimizes approximate MU is:
$$ \begin{equation*} \theta_{t+1}-\theta_t:\approx-\tilde\alpha_t \underbrace{(H_t^r)^{-1}}_{(R)} [ \underbrace{H^f_*(H_*^r)^{-1}}_{(S)} \underbrace{[-\nabla \mathcal L^f(\theta_t;\boldsymbol{\varepsilon}_t)]}_{(F)} ]. \end{equation*} $$($F$ ) represents the gradient ascent direction of the weighted forgetting loss, which directs the model to discard the information of the forgetting samples.
($R$ ) fine-tuning on the remaining set to sustain the model’s general capabilities.
($S$ ) amplifies the parameter updates crucial for forgetting, while dampens those important for maintaining.
Citation
If you find this work useful for your research, please consider citing:
@article{huang2024unified,
title={Unified Gradient-Based Machine Unlearning with Remain Geometry Enhancement},
author={Huang, Zhehao and Cheng, Xinwen and Zheng, JingHao and Wang, Haoran and He, Zhengbao and Li, Tao and Huang, Xiaolin},
journal={arXiv preprint arXiv:2409.19732},
year={2024}
}
